左邻域右邻域区别 左邻域和右领域符号表示

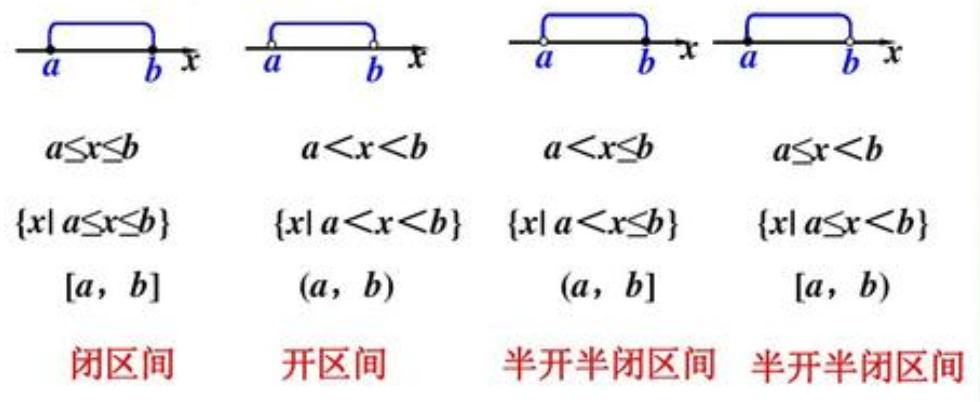
1、去心邻域就是无限接近于边界但是不包括边界的那一个级微小的范围左邻域右邻域区别，包括左邻域和右邻域，既然是邻域就说明它的范围很小，并且相邻，去心就是不包括那个比较点如a点的去心邻域，就是指a点左右的无限接近于a点但不包括a点的那一很微小的范围，一般出题时牵涉到去心邻域是，其实是为左邻域右邻域区别了说明在这一点；邻域是一个特殊的区间，以点a为中心点任何开区间称为点a的邻域，记作Ua点a的δ邻域设δ是一个正数，则开区间aδ，a+δ称为点a的δ邻域，点a称为这个邻域的中心，δ称为这个邻域的半径a的δ邻域去掉中心a后，称为点a的去心δ邻域，有时把开区间aδ，a称为a的左δ。

2、邻域指的是是无限小概念当会用到的， 即可以无限地接近的一个范围强调的内容是可以无限小，范围去心邻域指的是邻域内不包括某一个点 举个例来说，求0 的邻域是可以包括 0在内 的 但是求 0 的去心邻域是，是不包括 0 的在内的；此外，根据δ邻域的位置，还可以进一步定义左δ邻域和右δ邻域具体而言，开区间aδ，a被称为a的左δ邻域，而开区间a，a+δ则被称为a的右δ邻域这些定义在讨论函数行为时提供了额外的灵活性邻域的概念在数学分析微积分等领域有着广泛的应用通过这些定义，我们可以精确地描述函数在；2 判断极值点左右邻域的导数值的正负如果左邻域导数为正，右邻域导数为负，则该点为极大值点如果左邻域导数为负，右邻域导数为正，则该点为极小值点如果左右邻域导数符号相同，则该点不是极值点此外，极值的概念也可以应用于集合在一个有序集合中，如果存在一个元素其值大于其他所有元素；同样地，如果一个函数在某点的左导数存在，那么在该点的左侧邻域内，函数也是可导的，并且导数是连续的这意味着函数在该点左侧的行为也是可预测的如果一个函数的右导数和左导数都存在，那么我们可以推断出函数在那一点是连续的这个结论可以通过极限的定义来证明，即如果函数在某点的左极限和右极限；点a的去心δ邻域有时用到的邻域需要把邻域中心去掉，点a的δ邻域去掉中心a后，称为点a的去心δ邻域，记作表达方法是在U上标一个小的0，即，这里表示有时把开区间a δ， a称为a的左δ邻域，把开区间a， a + δ称为a的右δ邻域1。

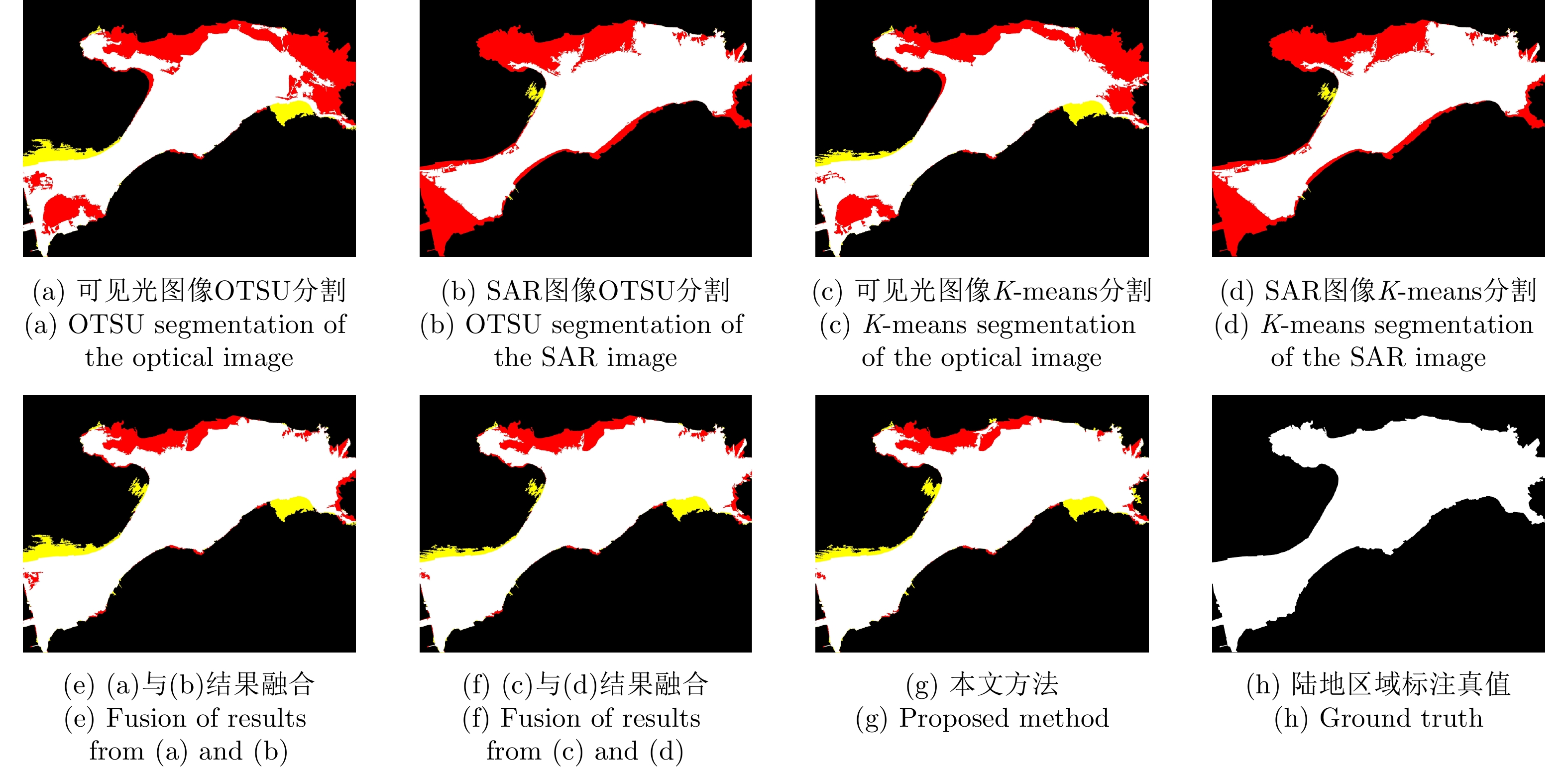
3、不相等去心邻域即在a的邻域中去掉a的数的集合，应用于高等数学去心邻域左右不相等邻域是使用无限小的概念并且可以无限接近的范围，强调的内容无限小，有范围，在高等数学中起着重要的作用；其实没有这个左邻域导数的说法 左邻域右邻域区别你一定要想的话，左邻域导数是一个区域的导数，也就是有无穷个点对应无穷个不同点的导数这叫做导函数左导数是什么意思，是针对一个特定的点，比如x0处，在定义域x无限趋近于x0的时候的导数通俗的说比如x=1处的导数就是 f #391，左导数就是趋近于1的时候；数轴上的点X0的δ邻域是指点集 NX0， δ = X XX0ltδ， δ0邻域内的点是由不等式 X0δ lt X lt X0+δ 界定的，包括X0点2 去心邻域数轴上的点X0的δ去心邻域是指点集NX0， δ = X 0ltXX0ltδ， δ0去心邻域与邻域的区别仅在于不包括X0点；先给结论，具体证明和细节看图1点x0的导数0，可以推出该点左邻域内所有函数值都比该点小，右邻域内都比该邻域大2区间内的单调性，需要区间内的导数都=0或者lt=0，一点的单调性并没有用PS感性认识单调性是比大小更强的结论，所以需要更强的条件；定义 以点 公式 为中心的任何开区间，都称为点 公式 的邻域，记为 公式 对任意公式 ， 开区间 公式 称为 公式 的 公式 邻域，记为 公式 ，其另一写法为公式 即到点公式 的距离小于 公式 的点的全体若去掉点公式 ， 即 公式 ，称为点 公式。

4、它的邻域可导，不能说明在他这点可导，你比如y的x绝对值在x为零的时候，左邻域右邻域，都可导的，但是在这点本身是不可导的，另外还有一种情况是在这个点没有定义，它左右都导，但是因为没有定义，所以该点不可导函数可导的条件1函数在该点的去心邻域内有定义2函数在该点处的左右；左极限就是函数从一个点的左侧无限靠近该点时所取到的极限值，且误差可以小到我们任意指定的程度，只需要变量从坐标充分靠近于该点右极限就是函数从一个点的右侧无限靠近该点时所取到的极限值，且误差可以小到我们任意指定的程度，只需要变量从坐标充分靠近于该点左极限与右极限统称单侧极限；区间邻域是一个特殊的区间，以点a为中心点任何开区间称为点a的邻域，点a的δ邻域设δ是一个正数，则开区间aδ，a+δ称为点a的δ邻域点a称为这个邻域的中心；一阶导数通常用于直线逼近曲线，而泰勒公式则使用高阶导数进行曲线逼近因此，泰勒公式在数值上更加精确，能够更好地反映函数在指定点附近的变化趋势适用条件泰勒公式适用于函数在某点及其附近足够光滑的情况如果函数在某点的左邻域或右邻域可导，则泰勒公式可以在单侧邻域内满足邻域概念邻域是指。